Chess-GPT's Internal World Model

A Chess-GPT Linear Emergent World Representation

Introduction

Note: This work has since been turned into a paper accepted to the Conference on Language Modeling, but the average reader will probably prefer the blog post. There is also a second blog post, Manipulating Chess-GPT’s World model.

Among the many recent developments in ML, there were two I found interesting and wanted to dig into further. The first was gpt-3.5-turbo-instruct’s ability to play chess at 1800 Elo. The fact that an LLM could learn to play chess well from random text scraped off the internet seemed almost magical. The second was Kenneth Li’s Emergent World Representations paper. There is an excellent summary on The Gradient and a follow-up from Neel Nanda. In it, they trained a 25 million parameter GPT to predict the next character in an Othello game. It learns to accurately make moves in games unseen in its training dataset, and using both non-linear and linear probes it was found that the model accurately tracks the state of the board.

However, this only worked for a model trained on a synthetic dataset of games uniformly sampled from the Othello game tree. They tried the same techniques on a model trained using games played by humans and had poor results. To me, this seemed like a major caveat to the findings of the paper which may limit its real world applicability. We cannot, for example, generate code by uniformly sampling from a code tree.

So I dug into it. I trained some models on chess games and used linear probes on the trained models. My results were very positive, and answered all of my previous questions (although of course, more questions were generated).

A 50 million parameter GPT trained on 5 million games of chess learns to play at ~1300 Elo in one day on 4 RTX 3090 GPUs. This model is only trained to predict the next character in PGN strings (1.e4 e5 2.Nf3 …) and is never explicitly given the state of the board or the rules of chess. Despite this, in order to better predict the next character, it learns to compute the state of the board at any point of the game, and learns a diverse set of rules, including check, checkmate, castling, en passant, promotion, pinned pieces, etc. In addition, to better predict the next character it also learns to estimate latent variables such as the Elo rating of the players in the game.

All code, data, and models have been open sourced.

Training Chess GPT

My initial hypothesis was that Othello-GPT trained on human games performed poorly due to a lack of data. They only had 130k human Othello games, but the synthetic model was trained on 20 million games. I tried two different approaches to create my datasets: First, I had Stockfish Elo 3200 play 5 million games as White against a range of Stockfish 1300-3200 as Black. Hopefully, this synthetic dataset of superhuman chess bot games would provide higher quality data than human games. Second, I grabbed 16 million games from Lichess’s public chess game database. I trained separate models on individual datasets and various mixes of datasets (more details in the appendix).

Initially, I looked at fine-tuning open source models like LLama 7B or OpenLlama 3B. However, I almost immediately had to abandon that approach to keep my GPU costs down (I used RTX 3090s from runpod). Instead, I started training models from scratch using Andrej Karpathy’s nanogpt repository. I experimented with 25M and 50M parameter models.

It basically worked on the first try. The 50M parameter model played at 1300 Elo with 99.8% of its moves being legal within one day of training. I find it fairly impressive that a model with only 8 layers can correctly make a legal move 80 turns into a game. I left one training for a few more days and it reached 1500 Elo. I’m still investigating dataset mixes and I’m sure there’s room for improvement.

So, gpt-3.5-turbo-instruct’s performance is not magic. If you give an LLM a few million chess games, it will learn to play chess. My 50M parameter model is orders of magnitude smaller than any reasonable estimate of gpt-3.5’s size, and it is within 300 Elo of its performance. In addition, we recently had confirmation that GPT-4’s training dataset included a collection of PGN format chess games from players with an Elo over 1800.

I also checked if it was playing unique games not found in its training dataset. There are often allegations that LLMs just memorize such a wide swath of the internet that they appear to generalize. Because I had access to the training dataset, I could easily examine this question. In a random sample of 100 games, every game was unique and not found in the training dataset by the 10th turn (20 total moves). This should be unsurprising considering that there are more possible games of chess than atoms in the universe.

Chess-GPT’s Internal World Model

Next, I wanted to see if my model could accurately track the state of the board. A quick overview of linear probes: We can take the internal activations of a model as it’s predicting the next token, and train a linear model to take the model’s activations as inputs and predict board state as output. Because a linear probe is very simple, we can have confidence that it reflects the model’s internal knowledge rather than the capacity of the probe itself. We can also train a non-linear probe using a small neural network instead of a linear model, but we risk being misled as the non-linear probe picks up noise from the data. As a sanity check, we also probe a randomly initialized model.

In the original Othello paper, they found that only non-linear probes could accurately construct the board state of “this square has a black / white / blank piece”. For this objective, the probe is trained on the model’s activations at every move. However, Neel Nanda found that a linear probe can accurately construct the state of the board of “this square has my / their / blank piece”. To do this, the linear probe is only trained on model activations as it’s predicting the Black XOR White move. Neel Nanda speculates that the nonlinear probe simply learns to XOR “I am playing white” and “this square has my color”.

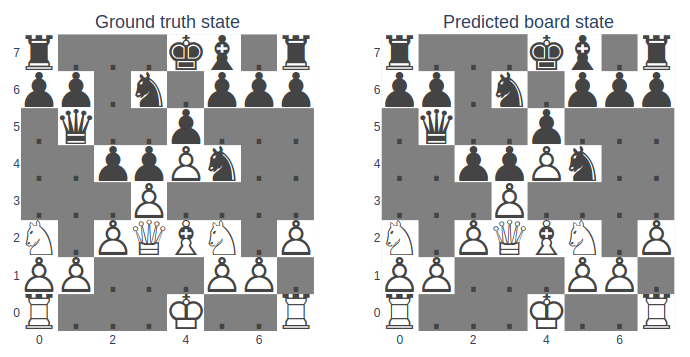
Armed with this knowledge, I trained some linear probes on my model. And once again, it basically worked on my first try. I also found that my Chess-GPT uses a “my / their” board state, rather than a “black / white” board state. My guess is that the model learns one “program” to predict the next move given a board state, and reuses the same “program” for both players. The linear probe’s objective was to classify every square into one of 13 classes (blank, white / black pawn, rook, bishop, knight, king, queen). The linear probe accurately classified 99.2% of squares over 10,000 games.

To better interpret the internal predictions of my model, I created some visual heat maps. These heat maps were derived from the probe outputs, which had been trained on a one-hot objective to predict whether a chess piece, such the black king, was present on a given square (1 if present, 0 if not). The first heat map shows the actual board state for the black king. The second heat map depicts the probe’s confidence with a clipping limit applied to the output values where any value above 5 is reduced to 5. This clipping makes the probe’s output more binary, as shown by the white square against the black background. The third heat map presents the probe’s output without any clipping, revealing a gradient of confidence levels. It shows that the model is extremely certain that the black king is not located on the white side of the chessboard.

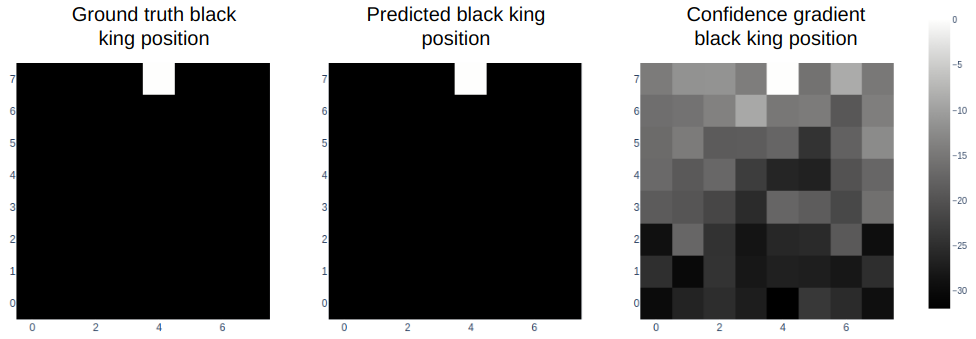
We see a very similar result for the location of the white pawns, although the model is less confident. This board state comes from the 12th move in a chess game, and the model is extremely confident that no white pawns are in either side’s back rank.

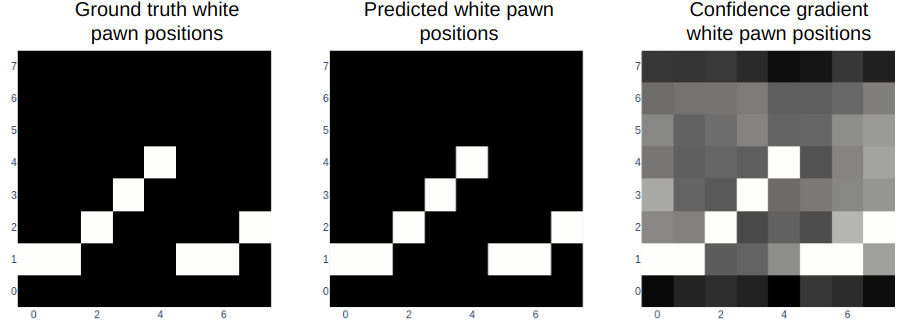
The model still knows where the blank squares are, but it is once again less confident in this.

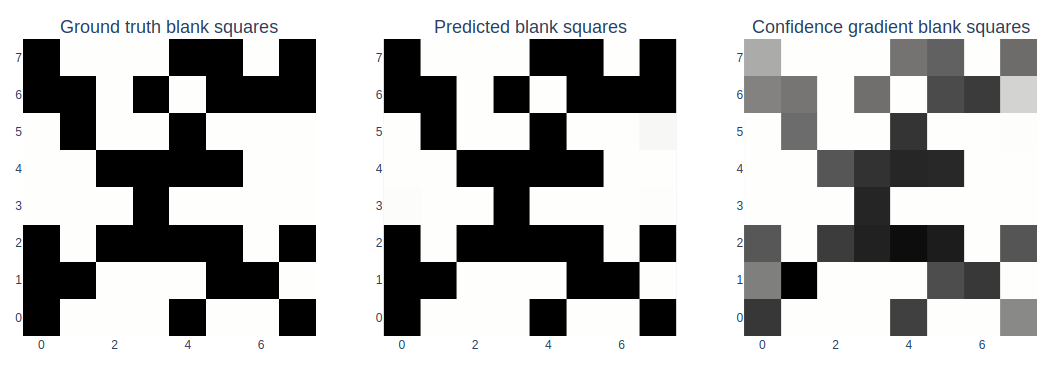
For this move in this chess game, the linear probe perfectly reconstructs the state of the board. The probe’s objective is to classify each square into one of 13 categories, each representing a different chess piece or a blank square. To create this graph, we just take the prediction with the highest value for each square as the probe’s output.

Probing for latent variables

Because Chess-GPT learned to predict the next move in a competitive game, rather than a game uniformly sampled from a game tree, there are interesting latent variables we can probe for. In particular, I hypothesized that to better predict the next character, it would learn to estimate the skill level of the players involved.

Initially, I trained the probe on a regression task, where its task is to predict the Elo of the White player. It would do this by training on the internal activations of the model between moves 25 and 35, as it would be extremely difficult to predict player skill early in the game. However, the majority of the games in the Lichess dataset are between 1500 Elo and 1880 Elo, which is a relatively narrow band¹. The linear probe trained on Chess-GPT had an average error of 150 Elo, which seemed good at first glance. However, a linear probe trained on a randomly initialized model had an average error of 215 Elo. The narrow window of Elo in most games made it difficult to discern the model’s level of knowledge. Distinguishing between a 1700 and 1900 Elo player just seems like a very difficult task.

So, I then trained the probe on a classification task, where it had to identify players below an Elo of 1516 or above an Elo of 2029. In this case, the probe performed much better. A probe trained on a randomly initialized model correctly classified 66% of players, while a probe trained on Chess-GPT correctly classified 89% of players.

To an extent, this is unsurprising. This reminds me of the OpenAI’s 2017 Sentiment Neuron paper. In it, they trained an LSTM to predict the next character in Amazon reviews. When they trained a linear probe on the model’s internals using just 232 labeled examples, it became a state of the art sentiment classifier. OpenAI wrote then that “We believe the phenomenon is not specific to our model, but is instead a general property of certain large neural networks that are trained to predict the next step or dimension in their inputs”. With this context, it’s almost an expected result.

Caveats

The evidence here would be stronger if I also performed causal interventions on the model using these probes. For example, I could intervene to change the model’s internal representation of the board state, and see if it makes legal moves under the new state of the board. Or, I could intervene on the model’s representation of player skill and see if it plays better or worse. Unfortunately, I just ran out of time. This was a Christmas break project, and it’s time to get back to work.

However, I still consider the findings to be strong. Linear probes have a limited capacity, and are an accepted method of benchmarking what a model has learned. I followed general best practices of training the probes on a training set, and testing them on a separate test set. The board state in particular is a very concrete task to probe against. Probing for skill level does have a possibility that the model is learning some feature that is mostly correlated with skill, but 89% is a good result for the difficult task of discerning the Elo of players in a chess game after 25 moves.

Potential future work

As Neel Nanda discussed, there are many advantages to interpreting models trained on narrow, constrained tasks such as Othello or Chess. It is difficult to interpret what a large LLM like Llama is modeling internally when predicting tokens in an unconstrained domain like poetry. There has been successful interpretation of simple models trained on toy tasks like sorting a list. Models trained on games provide a good intermediate step that is both tractable and interesting.

My immediate thought is to look for some sort of internal tree search. When I play chess, I perform a sort of tree search, where I first consider a range of moves, then consider my opponent’s responses to these moves. Does Chess-GPT perform a similar internal calculation when predicting the next character? Considering that it is better than I am, it seems plausible.

Other potential directions:

• Perform causal interventions on the model using these linear probes.
• Investigate why the model sometimes fails to make a legal move or model the true state of the board.
• How does the model compute the state of the board, or the location of a specific piece?
• I fine-tuned GPT-2 on a 50 / 50 mix of OpenWebText and chess games, and it learned to play chess and continued to output plausible looking text. Maybe there’s something interesting to look at there?

Part two: Manipulating Chess-GPT’s World Model

If interested in discussion or collaboration, feel free to contact me via email. There is also this Twitter thead for public discussion purposes.

I am currently open to job opportunities. If you found this post interesting and think I could be a good fit for your team, feel free to reach out via email or LinkedIn.

Appendix

Corrections

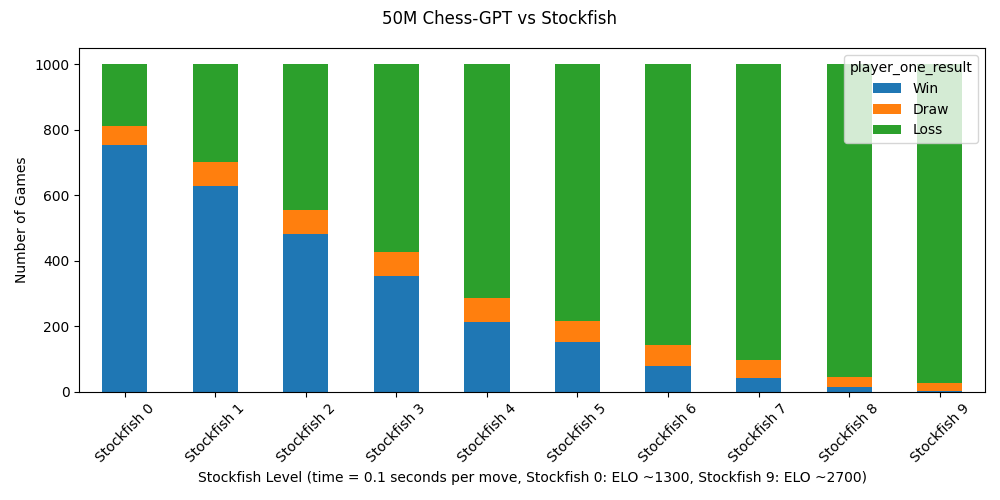
In my original article, I had a graph with a stacked bar chart of Chess-GPT’s games against Stockfish, with bars for wins, draws, and losses. I noticed that there was an unusually high amount of draws against Stockfish levels 5 through 9. After some inspection, I realized that I had mistakenly inflated the draw rate. The cause was the following: Chess-GPT has an context size of 1024 characters, enough for approximately 180 moves. My analysis code mistakenly categorized an active game at 180 moves as a draw. While a game at 180 moves is more likely to result in a draw than average, it definitely isn’t certain. I used the following strategy to redo the graph: At every active game, I used Stockfish to assign a centipawn advantage at move 180. Any player with more than 100 centipawn advantage received a win. All other games were a draw. 77% of these games were Stockfish wins. The old, inaccurate bar graph can be viewed here and the old, inaccurate line chart can be viewed here. This does not change the Elo rating of Chess-GPT, but it’s definitely a mistake for which I apologize.

Updates

2024/03/23: I wrote up the results of this blog post in a paper titled “Emergent World Models and Latent Variable Estimation in Chess-Playing Language Models”. I reran some of the experiments here with larger sample sizes to improve rigor (for example, Chess-GPT was benchmarked with 1,000 games against Stockfish, not 100). I also improved the quality of some figures, and used log probabilities in my probe heatmaps instead of logits. I also added an appendix section discussing Stockfish Elo estimation.

Technical probing details

Both Neel Nanda and I trained our probes to predict “my piece / their piece” instead of “white piece / black piece”. To predict “white piece / black piece”, you just have to train the linear probe on the model’s activations at every move. To predict “my piece / their piece”, you have to train the linear probe on the model’s activations at every white XOR black move.

In Othello-GPT, the model had a vocabulary of 60 tokens, corresponding to the 60 legal squares where a piece could be placed. So, Neel Nanda just probed at every even character for a white “my piece / their piece” probe, and at every odd character for a black “my piece / their piece” probe. In my case, the input to Chess-GPT was a string like “1.e4 e5 2.Nf3 …”.

So, I trained the white “my piece / their piece” probe on the model’s activations at the index of every “.” as it’s predicting the next character. For example, the probe would be trained on “1.” and “1.e4 e5 2.” as inputs. For a black “my piece / their piece” probe, I trained it on the index of every even “ “ character. I trained a linear probe on the “white piece / black piece” objective, and it obtained a classification accuracy of 86%.

Neel Nanda excluded the first 5 and last 5 moves of the game when training his probes. I found that my linear probes accuracy did not change when trained on all moves or all but the first 5 moves.

Model training details

The LLMs were character level models rather than using byte-pair encoding and tokenization. From manually inspecting gpt-3.5 tokenization, it looks like a standard tokenizer has slightly over 1 character per token for a PGN string, excluding spaces. As my model had a vocabulary of just 32 tokens, I was able to reduce my model size by 25 million parameters compared to using a standard tokenizer with a vocabulary of 50,257 tokens. During training, I ensured that every batch began with “;1.”, a delimiter token followed by a new game. I did try training a model by randomly sampling blocks that usually began in the middle of a game, although its 1024 context length meant that it usually also received the beginning of a game later on. The model still learned to play chess. I would be curious what sort of heuristics that model learned to infer the board state when receiving an input that starts in the middle of a chess game.

Open source code, models, and datasets

All code, models, and datasets are open source. To train, test, or visualize linear probes on the LLMs, please visit: https://github.com/adamkarvonen/chess_llm_interpretability

To play the nanoGPT model against Stockfish, please visit: https://github.com/adamkarvonen/chess_gpt_eval/tree/master/nanogpt

To train a Chess-GPT from scratch, please visit: https://github.com/adamkarvonen/nanoGPT

All pretrained models are available here: https://huggingface.co/adamkarvonen/chess_llms

All datasets are available here: https://huggingface.co/datasets/adamkarvonen/chess_games

Wandb training loss curves and model configs can be viewed here: https://api.wandb.ai/links/adam-karvonen/u783xspb

Model size and dataset comparison

Model Name	Probe Layer Target	Elo Classification Accuracy	Board State Classification Accuracy	Legal Move Rate
Randomly Initialized 8 layer model	5	65.8%	70.8%	0%
Randomly Initialized 16 layer model	12	66.5%	70.6%	0%
8 Layer Model trained on Lichess Games	7	88.0%	98.0%	99.6%
16 Layer Model trained on Lichess Games	12	89.2%	98.6%	99.8%
16 Layer Model trained on Stockfish Games	12	N/A	99.2%	99.7%

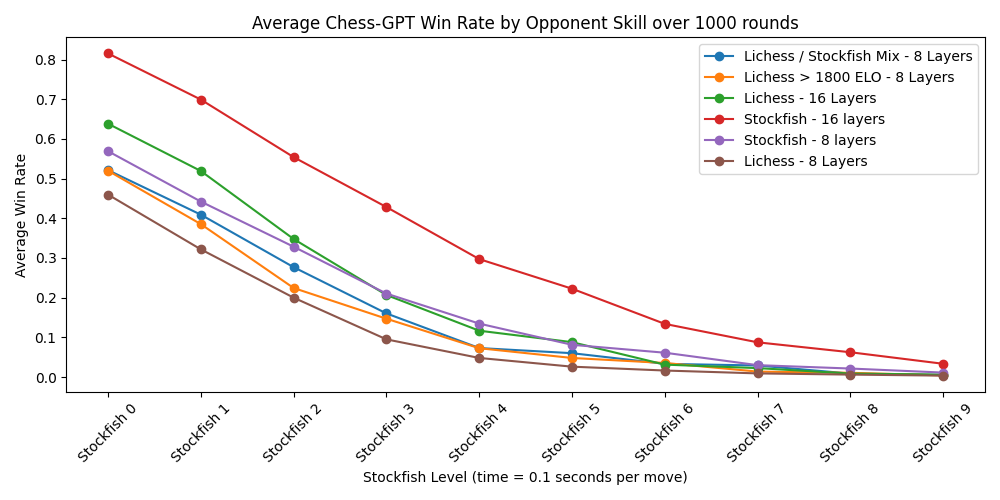
All models were trained for a total of 60 billion input characters. The models were trained for several epochs - the datasets ranged in size from 4 - 7 billion characters. The labels stand for the dataset from hugging face that the model was trained on as well as the number of layers in the model. In this graph, for 1 game a win counts as 1 point, a draw as 0.5, and a loss as 0. We lose some information compared to a stacked bar chart, but I felt it would be too crowded.

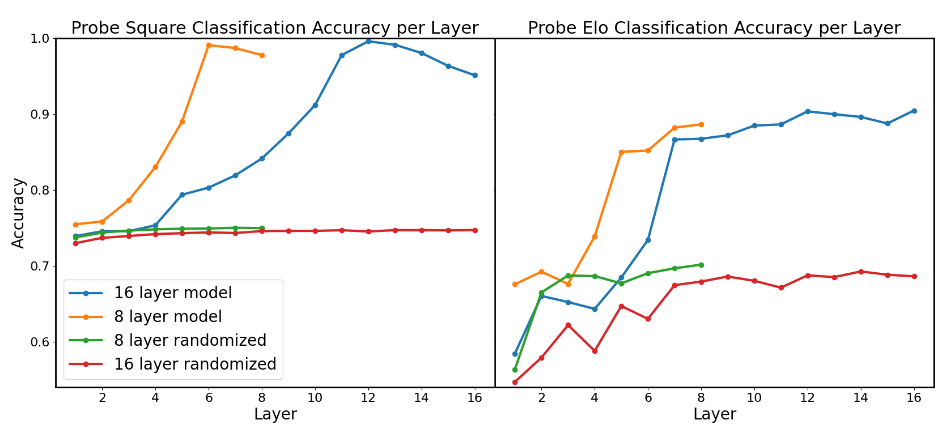
Probe accuracy per layer on in 8 and 16 layer networks

An interesting note: The 8 layer network can calculate a 98% accurate board state by layer 5. However, the 16 layer network doesn’t calculate an accurate board state until layer 11. This indicates that the network is calculating many things in parallel, rather than calculating the board state as soon as possible and then planning from there. Oddly, the skill probes trained on randomized models become more accurate on deeper layers.

Stockfish Elo Estimate

Elo estimation of Stockfish levels is complex with several variables at play. An official estimate of Stockfish 16 Elos can be obtained in a commit on the official Stockfish repo. In this case, Stockfish 16 level 0 is Elo 1,320. The official Stockfish testing was performed using 120 seconds per move, which is prohibitively expensive for tens of thousands of games on GPU machines. The particular processor being used per machine is another variable.

To estimate the Elo of Stockfish level 0 at 0.1 seconds per move, I had it play 1,000 games as white against Stockfish level 0 with 0.1, 1.0 and 10.0 seconds per move. The win rate of 0.1 vs 0.1 seconds was 51%, 0.1 vs 1.0 seconds was 45%, and 0.1 vs 10.0 seconds was 45%. At low Stockfish levels, a 100x decrease in search time makes little difference in Stockfish’s win rate. In contrast, at higher Stockfish levels, decreasing search time makes a significant difference in win rate. Thus, a reasonable approximation of Stockfish 16 level 0 with 0.1 seconds per move is Elo 1300.

1. Lichess’s Elo ratings appear to run high. The average chess.com Elo is around 800. A quick google shows that many believe Lichess ratings are on average a few hundred Elo higher than other websites’ Elo ratings. ↩